2016年8月5日星期五

阮一峰的网络日志

阮一峰的网络日志

布尔代数入门

Posted: 04 Aug 2016 05:17 PM PDT

布尔代数是计算机的基础。没有它，就不会有计算机。

布尔代数发展到今天，已经非常抽象，但是它的核心思想很简单。本文帮助你理解布尔代数，以及为什么它促成了计算机的诞生。

我依据的是《编码的奥妙》的第十章。这是一本好书，强烈推荐。

一、数理逻辑的起源

18世纪早期，英国数学家乔治·布尔（George Boole，1815－1864）突发奇想：人的思想能不能用数学表达？

此前，数学只用于计算，没有人意识到，数学还能表达人的逻辑思维。

两千年来，哲学书都是用文字写的。比如，最著名的三段论：

所有人都是要死的，
苏格拉底是人，
所以，苏格拉底是要死的。

乔治·布尔认为，这种推理可以用数学表达，也就是说，哲学书完全可以用数学写。这就是数理逻辑的起源。

二、集合论

乔治·布尔发明的工具，叫做"集合论"（Set theory）。他认为，逻辑思维的基础是一个个集合（Set），每一个命题表达的都是集合之间的关系。

比如，所有人类组成一个集合R，所有会死的东西组成一个集合D。

所有人都是要死的

集合论的写法就是：

R X D = R

集合之间最基本的关系是并集和交集。乘号（X）表示交集，加号（+）表示并集。上面这个式子的意思是，R与D的交集就是R。

同样的，苏格拉底也是一个集合S，这个集合里面只有苏格拉底一个成员。

苏格拉底是人
// 等同于
S X R = S

上面式子的意思是，苏格拉底与人类的交集，就是苏格拉底。

将第一个式子代入第二个式子，就得到了结论。

S X (R X D)
= (S X R) X D
= S X D
= S

这个式子的意思是，苏格拉底与会死的东西的交集，就是苏格拉底，即苏格拉底也属于会死的东西。

三、集合的运算法则

前面的三段论比较容易，一眼就能看出结论。但是，有些三段轮比较复杂，不容易立即反应过来。

请看下面这两句话。

"鸭嘴兽是卵生的哺乳动物。鸭嘴兽是澳洲的动物。"

你能一眼得到结论吗？

鸭嘴兽 X 卵生 = 鸭嘴兽
鸭嘴兽 x 澳洲 = 鸭嘴兽

将第一个式子代入第二个，就会得到：

鸭嘴兽 X 卵生 x 澳洲 = 鸭嘴兽
// 相当于
卵生 x 澳洲 = 鸭嘴兽 + 其他

因此，结论就是"有的卵生动物是澳洲的动物"，或者"有的澳洲的动物是卵生动物"。

还有更不直观的三段论。

"哲学家都是有逻辑头脑的，一个没有逻辑头脑的人总是很顽固。"

请问结论是什么？

这道题会用到新的概念：全集和空集。集合A和所有不属于它的元素（记作-A）构成全集（I），这时A和-A的交集就是一个空集（0）。

A + (-A) = I
A X (-A) = 0

因此，有下面的公式。

B
= B X I
= B X (A + -A)
= B X A + B X (-A)

回到上面那道题。

哲学家 X 逻辑 = 哲学家
无逻辑 X 顽固 = 无逻辑

根据第一个命题，可以得到下面的结论。

哲学家 X 无逻辑
= (哲学家 X 逻辑) X 无逻辑
= 哲学家 X (逻辑 X 无逻辑)
= 哲学家 X 0
= 0

即哲学家与没有逻辑的人的交集，是一个空集。

根据第二个命题，可以得到下面的结论。

无逻辑 X 顽固
= 无逻辑 X 顽固 X (哲学家 + 非哲学家)
= 无逻辑 X 顽固 X 哲学家 + 无逻辑 X 顽固 X 非哲学家
= 0 X 顽固 + 无逻辑 X 顽固 X 非哲学家
= 无逻辑 X 顽固 X 非哲学家
= 无逻辑

也就是说，最终的结论如下。

无逻辑 X 顽固 X 非哲学家 = 无逻辑
// 相当于
顽固 X 非哲学家 = 无逻辑 + 其他

结论就是顽固的人与非哲学家之间有交集。通俗的表达就是：一些顽固的人，不是哲学家，或者一些不是哲学家的人，很顽固。

由此可见，集合论可以帮助我们得到直觉无法得到的结论，保证推理过程正确，比文字推导更可靠。

四、 集合论到布尔代数

既然命题可以用集合论表达，那么逻辑推导无非就是一系列集合运算。

由于集合运算的结果还是集合，那么通过判断个体是否属于指定集合，就可以计算命题的真伪。

一名顾客走进宠物店，对店员说："我想要一只公猫，白色或黄色均可；或者一只母猫，除了白色，其他颜色均可；或者只要是黑猫，我也要。"

这名顾客的要求用集合论表达，就是下面的式子。

公猫 X (白色 + 黄色)
+ 母猫 X 非白色
+ 黑猫

店员拿出一只灰色的公猫，请问是否满足要求？

布尔代数规定，个体属于某个集合用1表示，不属于就用0表示。 灰色的公猫属于公猫集合，就是1，不属于白色集合，就是0。

上面的表达式变成下面这样。

1 X (0 + 0)
+ 0 X 1
+ 0
= 0

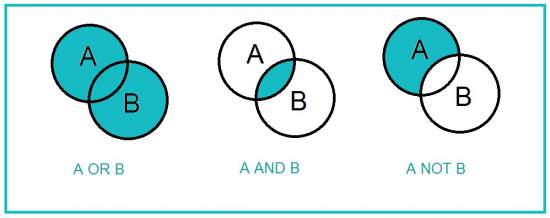
因此，就得到结论，灰色的公猫不满足要求。

这就是布尔代数：计算命题真伪的数学方法。

五、布尔代数的运算法则

布尔代数的运算法则与集合论很像。

交集的运算法则如下。

1 X 1 = 1
1 X 0 = 0
0 X 0 = 0

并集的运算法则如下。

1 + 1 = 1
1 + 0 = 1
0 + 0 = 0

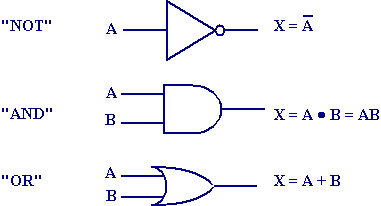
集合论可以描述逻辑推理过程，布尔代数可以判断某个命题是否符合这个过程。人类的推理和判断，因此就变成了数学运算。

20世纪初，英国科学家香农指出，布尔代数可以用来描述电路，或者说，电路可以模拟布尔代数。于是，人类的推理和判断，就可以用电路实现了。这就是计算机的实现基础。

六、布尔代数的局限

虽然布尔代数可以判断命题真伪，但是无法取代人类的理性思维。原因是它有一个局限。

它必须依据一个或几个已经明确知道真伪的命题，才能做出判断。比如，只有知道"所有人都会死"这个命题是真的，才能得出结论"苏格拉底会死"。

布尔代数只能保证推理过程正确，无法保证推理所依据的前提是否正确。如果前提是错的，正确的推理也会得到错误的结果。而前提的真伪要由科学实验和观察来决定，布尔代数无能为力。

（完）

文档信息
发帖者 时间：